Implements the second order derivative term of cost function. More...

#include <SecondDerivativeCostFunction.hpp>

Inheritance diagram for julian::ir::SecondDerivativeCostFunction:

Public Member Functions
	SecondDerivativeCostFunction (SmartPointer< SmootherCostFunction > c, double weight=1.0)
	Constructor. More...

virtual arma::mat	giveQmatrix (const InterpolatedCurve &) const
	returns Q matrix, the quadratic term of optimization cost function More...

virtual arma::mat	giveCvector (const InterpolatedCurve &) const
	returns C vector More...

virtual double	calculateCost (const InterpolatedCurve &) const
	returns curve as vector of doubles More...

virtual SecondDerivativeCostFunction *	clone () const
	virtual copy constructor More...

Public Member Functions inherited from julian::ir::CostFunctionDecorator
	CostFunctionDecorator (SmartPointer< SmootherCostFunction > c)
	Constructor. More...

virtual std::vector< double >	giveSmoothedCurve (const InterpolatedCurve &) const
	returns curve as vector of doubles More...

virtual void	updateSmoothedCurve (InterpolatedCurve &, const std::vector< double > &) const
	updates the curve as with the vector of doubles More...

virtual	~CostFunctionDecorator ()
	destructor More...

Public Member Functions inherited from julian::ir::SmootherCostFunction
	SmootherCostFunction ()
	constructor More...

virtual	~SmootherCostFunction ()
	destructor More...

Private Attributes
double	weight_
	Weight assigned to second order term (see parameter b in equation above) More...

Additional Inherited Members
Protected Member Functions inherited from julian::ir::CostFunctionDecorator
arma::mat	matrixD (int size, int order) const
	Creates matrix representation of differential operator. More...

arma::mat	matrixX (const InterpolatedCurve &c, int order) const
	Creates matrix representation of differential operator. More...

Detailed Description

Implements the second order derivative term of cost function.

$Cost_{f} =a \int^{tN}_{t0} \Big(\frac{df(x)}{dx}\Big)^2 dx + \underline{b \int^{T}_t \Big(\frac{df^2(x)}{dx^2}\Big)^2 dx}$

The integral is evaluated numerically:

$\int^{tN}_{t0} \Big(\frac{df^2(x)}{dx^2}\Big)^2 dx \approx \sum^{i=N-2}_{i=0}\Big(\frac{x(t_{i+2})- 2x(t_{i+1}) + x(t_{i})}{(t_{i+2}-t_i)^2}\Big)^2 = x^T D^T_2D_2 x = x^T Q x$

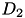where $D_2$ is a matrix representing second order differentiation and 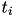$t_i$ are grid dates of the curve.

Examples:: bootstrapperComparison.cpp, constrainedBootstrapperExample.cpp, and unconstrainedBootstrapperExample.cpp.

Constructor & Destructor Documentation

julian::ir::SecondDerivativeCostFunction::SecondDerivativeCostFunction	(	SmartPointer< SmootherCostFunction >	c,
		double	weight = `1.0`
	)

inlineexplicit

Constructor.

Member Function Documentation

double julian::ir::SecondDerivativeCostFunction::calculateCost ( const InterpolatedCurve & input ) const

virtual

returns curve as vector of doubles

$Cost = \int^{tN}_{t0} \Big(\frac{df^2(x)}{dx^2}\Big)^2 dx$

InterpolatedCurve may be represented by different

Reimplemented from julian::ir::CostFunctionDecorator.

SecondDerivativeCostFunction * julian::ir::SecondDerivativeCostFunction::clone ( ) const

virtual

virtual copy constructor

Reimplemented from julian::ir::CostFunctionDecorator.

arma::mat julian::ir::SecondDerivativeCostFunction::giveCvector ( const InterpolatedCurve & input ) const

virtual

returns C vector

Method does not modify the C vector obtained from decorated class.

Reimplemented from julian::ir::CostFunctionDecorator.

arma::mat julian::ir::SecondDerivativeCostFunction::giveQmatrix ( const InterpolatedCurve & input ) const

virtual

returns Q matrix, the quadratic term of optimization cost function

Numerical derivative of a function f can be approximated using following formula

$\frac{d^2f(x)}{dx^2}|_{x=x_i} \approx \frac{f(x_{i+1}) - 2f(x_{i}) + f(x_{i-1})}{x_{i+1}-x_{i-1}}$

If $F = [f(x_1), f(x_2), ..., f(x_n)]$ then differencing of function can be presented in matrix form:

$\frac{dF}{sX} = X^{-1} \times D_{2} \times F$

where:

$D_{2} = \begin{bmatrix} 0 & 0 & 0 & 0 & \dots & 0 & 0 \\ 0 & 0 & 0 & 0 & \dots & 0 & 0 \\ 1 &-2 & 1 & 0 & \dots & 0 & 0 \\ 0 & 1 &-2 & 1 & \dots & 0 & 0 \\ \hdotsfor{7} \\ 0 & 0 & 0 & \dots & 1 & -2 & 1 \end{bmatrix}$

$X = \begin{bmatrix} x_{2} - x_{0} & 0 & 0 & \dots & 0 & 0 \\ 0 & x_{3} - x_{1} & 0 & \dots & 0 & 0 \\ 0 & 0 & x_{4} - x_{2} & \dots & 0 & 0 \\ 0 & 0 & 0 & \dots & 0 & 0 \\ \hdotsfor{6} \\ 0 & 0 & 0 &\dots & 0 & x_{n}-x_{n-2} \end{bmatrix}$

To calculate Q matrix InterpolatedCurve is needed,because we need the gird dates and the size of the curve

Parameters

input InterpolatedCurve for which Q matrix is calculated

Reimplemented from julian::ir::CostFunctionDecorator.

Member Data Documentation

double julian::ir::SecondDerivativeCostFunction::weight_

private

Weight assigned to second order term (see parameter b in equation above)

The documentation for this class was generated from the following files:

C:/Unix/home/OEM/jULIAN/src/marketData/interestRateCurves/estimators/costFunctions/SecondDerivativeCostFunction.hpp
C:/Unix/home/OEM/jULIAN/src/marketData/interestRateCurves/estimators/costFunctions/SecondDerivativeCostFunction.cpp

Public Member Functions

Private Attributes

Additional Inherited Members

Detailed Description

Constructor & Destructor Documentation

Member Function Documentation

Member Data Documentation