Implements the first order derivative term of cost function. More...
#include <FirstDerivativeCostFunction.hpp>
Public Member Functions | |
| FirstDerivativeCostFunction (SmartPointer< SmootherCostFunction > c, double weight=1.0) | |
| Constructor. More... | |
| virtual arma::mat | giveQmatrix (const InterpolatedCurve &) const |
| returns Q matrix, the quadratic term of optimization cost function More... | |
| virtual arma::mat | giveCvector (const InterpolatedCurve &) const |
| returns C vector More... | |
| virtual double | calculateCost (const InterpolatedCurve &) const |
| returns curve as vector of doubles More... | |
| virtual FirstDerivativeCostFunction * | clone () const |
| virtual copy constructor More... | |
 Public Member Functions inherited from julian::ir::CostFunctionDecorator | |
| CostFunctionDecorator (SmartPointer< SmootherCostFunction > c) | |
| Constructor. More... | |
| virtual std::vector< double > | giveSmoothedCurve (const InterpolatedCurve &) const |
| returns curve as vector of doubles More... | |
| virtual void | updateSmoothedCurve (InterpolatedCurve &, const std::vector< double > &) const |
| updates the curve as with the vector of doubles More... | |
| virtual | ~CostFunctionDecorator () |
| destructor More... | |
| Public Member Functions inherited from julian::ir::SmootherCostFunction | |
| SmootherCostFunction () | |
| constructor More... | |
| virtual | ~SmootherCostFunction () |
| destructor More... | |
Private Attributes | |
| double | weight_ |
| Weight assigned to first order term (see parameter a in equation above) More... | |
Additional Inherited Members | |
| Protected Member Functions inherited from julian::ir::CostFunctionDecorator | |
| arma::mat | matrixD (int size, int order) const |
| Creates matrix representation of differential operator. More... | |
| arma::mat | matrixX (const InterpolatedCurve &c, int order) const |
| Creates matrix representation of differential operator. More... | |
Detailed Description
Implements the first order derivative term of cost function.
![\[Cost_{f} = \underline{a \int^{tN}_{t0} \Big(\frac{df(x)}{dx}\Big)^2 dx} + b \int^{tN}_{t0} \Big(\frac{df^2(x)}{dx^2}\Big)^2 dx \]](form_53.png)
The integral is evaluated numerically:
![\[ \int^{tN}_{t0} \Big(\frac{df(x)}{dx}\Big)^2 dx \approx \sum^{i=N-1}_{i=0}\Big(\frac{x(t_{i+1}) - x(t_{i})}{t_{i+1}-t_i}\Big)^2 = x^T D^T_1D_1 x = x^T Q x\]](form_54.png)
where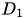 
is a matrix representing first order differentiation and 
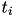are grid dates of the curve.
If this factor is used as the only one in the estimation process of the curve, it is equivalent to the estimating the curve with the smallest length.
Constructor & Destructor Documentation
|
inlineexplicit |
Constructor.
Member Function Documentation
|
virtual |
returns curve as vector of doubles
![\[ Cost = \int^{tN}_{t0} \Big(\frac{df(x)}{dx}\Big)^2 dx\]](form_52.png)
InterpolatedCurve may be represented by different
Reimplemented from julian::ir::CostFunctionDecorator.
|
virtual |
virtual copy constructor
Reimplemented from julian::ir::CostFunctionDecorator.
|
virtual |
returns C vector
Method does not modify the C vector obtained from decorated class.
Reimplemented from julian::ir::CostFunctionDecorator.
|
virtual |
returns Q matrix, the quadratic term of optimization cost function
Numerical derivative of a function f can be approximated using following formula
![\[\frac{df(x)}{dx}|_{x=x_i} \approx \frac{f(x_{i+1}) - f(x_{i})}{x_{i+1}-x_{i}}\]](form_46.png)
If ![$F = [f(x_1), f(x_2), ..., f(x_n)]$](form_47.png)
then differencing of function can be presented in matrix form:
![\[\frac{dF}{dX} = X^{-1} \times D_{1} \times F\]](form_51.png)
where:
![\[ D_{1} = \begin{bmatrix} 0 & 0 & 0 & \dots & 0 & 0 \\ -1 & 1 & 0 & \dots & 0 & 0 \\ 0 & -1 & 1 & \dots & 0 & 0 \\ 0 & 0 &-1 & \dots & 0 & 0 \\ \hdotsfor{6} \\ 0 & 0 & 0 & \dots & -1 & 1 \end{bmatrix}\]](form_49.png)
![\[ X = \begin{bmatrix} x_{1} - x_{0} & 0 & 0 & \dots & 0 & 0 \\ 0 & x_{2} - x_{1} & 0 & \dots & 0 & 0 \\ 0 & 0 & x_{3} - x_{2} & \dots & 0 & 0 \\ 0 & 0 & 0 & \dots & 0 & 0 \\ \hdotsfor{6} \\ 0 & 0 & 0 &\dots & 0 & x_{n}-x_{n-1} \end{bmatrix}\]](form_50.png)
To calculate Q matrix InterpolatedCurve is needed,because we need the gird dates and the size of the curve
- Parameters
-
input InterpolatedCurve for which Q matrix is calculated
Reimplemented from julian::ir::CostFunctionDecorator.
Member Data Documentation
|
private |
Weight assigned to first order term (see parameter a in equation above)
The documentation for this class was generated from the following files:
- C:/Unix/home/OEM/jULIAN/src/marketData/interestRateCurves/estimators/costFunctions/FirstDerivativeCostFunction.hpp
- C:/Unix/home/OEM/jULIAN/src/marketData/interestRateCurves/estimators/costFunctions/FirstDerivativeCostFunction.cpp
