Class implements Simulated Annealing minimizer. More...

#include <simulatedAnnealing.hpp>

Public Member Functions
	SimulatedAnnealing (SmartPointer< UniformRNG > rng, SmartPointer< RandomVariable > rand)
	Constructor. More...

void	setCoolingSchedule (const std::vector< double > &cooling_schedule)
	Set cooling schedule. More...

void	setLinearCooling (double Tstart, double Tend, double param)
	Calculates linear cooling schedule. More...

void	setExponentialCooling (double Tstart, double Tend, double param)
	Calculates exponential cooling schedule. More...

template<typename F , typename PA >
double	calculate (F f, PA prob_accept, double x_initial, int iters_per_t)
	Method finds the minimum of provided function. More...

template<typename F , typename PA >
std::vector< double >	calculate (F f, PA prob_accept, std::vector< double > x_initial, int iters_per_t)
	Method finds the minimum of provided function. More...

double	takeStep (double x)
	Calculate the new state. More...

std::vector< double >	takeStep (std::vector< double > x)
	Calculate the new state. More...

	~SimulatedAnnealing ()
	Destructor. More...

Private Attributes
SmartPointer< RandomVariable >	step_
	Distribution used in picking of neighbour state. More...

SmartPointer< UniformRNG >	rng_
	Random number generator used in acceptance of new state. More...

std::vector< double >	cooling_schedule_
	Cooling schedule. More...

Detailed Description

Class implements Simulated Annealing minimizer.

Simulating annealing is a stochastic algorithm used to solve optimization problems.

Quoting authors of Numerical Recipes (Chapter 10.9 [4]):

At the heart of the method of simulated annealing is an analogy with thermodynamics, specifically with the way that liquids freeze and crystallize, or metals cool and anneal. At high temperatures, the molecules of a liquid move freely with respect to one another. If the liquid is cooled slowly, thermal mobility is lost. The atoms are often able to line themselves up and form a pure crystal that is completely ordered over a distance up to billions of times the size of an individual atom in all directions. This crystal is the state of minimum energy for this system.

The pseudo-code of simulated annealing's algorithm is presented below:

x = initial guess
x_best = x
E = f(x)
E_best = E
for temperature in cooling_schedule:
    iter = 0
    while iter < maximum number of steps:
       x_new = pick a neighbour of x
       E_new = f(x_new) 

       if E_new <= E_best:
           x_best = x_new
           E_best = E_new
       
       if E_new < E:
           x = x_new
           E = E_new
       else if ( U(0,1) < acceptance_probability(E, E_new, T)
           x = x_new
           E = E_new
        
   iter++

Cooling schedule is a series of decreasing real numbers. The temperature influences the acceptance probability. For more details see [46]

The neighbour is picked from distribution provided by user. The distribution expected value should be equal to zero. Usually it is a normal or uniform distribution.

Acceptance probability is the probability of moving to a new state. If new steps is a step of lower energy the probability of taking the step is 1.0. In other case the probability is calculated using the acceptance probability function and compared to randomly picked number from standard uniform distribution. It means that algorithm can choose the non-optimal state, what makes the algorithm immune to local minimums. Larger increases in energy of the system should be less probably. The probability of such steps should decrease with temperature of the system. Kirkpatrick et al. choose the Boltzmann distribution: 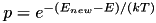$p = e^{-(E_{new} - E)/(kT)}$ , justified by analogy with the transitions of a physical systems. It also corresponds to the Metropolis–Hastings algorithm (see [44]). The implemented algorithm enables usage of any acceptance probability.

For more details see also: [11] [33] [38]

Examples:: simulatedAnnealingExample.cpp.

Constructor & Destructor Documentation

julian::SimulatedAnnealing::SimulatedAnnealing	(	SmartPointer< UniformRNG >	rng,
		SmartPointer< RandomVariable >	rand
	)

inline

Constructor.

julian::SimulatedAnnealing::~SimulatedAnnealing ( )

inline

Destructor.

Member Function Documentation

template<typename F , typename PA >

double julian::SimulatedAnnealing::calculate	(	F	f,
		PA	prob_accept,
		double	x_initial,
		int	iters_per_t
	)

Method finds the minimum of provided function.

Parameters

f	One-dimensional function which optimum we are looking for. f should be a functor.
prob_accept	Probability acceptance function
x_initial	Initial guess
iters_per_t	Number of iterations taken for each temperature value

Returns: the x for which function f obtains its minimum

Examples:: simulatedAnnealingExample.cpp.

template<typename F , typename PA >

std::vector< double > julian::SimulatedAnnealing::calculate	(	F	f,
		PA	prob_accept,
		std::vector< double >	x_initial,
		int	iters_per_t
	)

Method finds the minimum of provided function.

Parameters

f	Multi-dimensional function which optimum we are looking for. f should be a functor.
prob_accept	Probability acceptance function
x_initial	Initial guess
iters_per_t	Number of iterations taken for each temperature value

Returns: the x for which function f obtains its minimum

void julian::SimulatedAnnealing::setCoolingSchedule ( const std::vector< double > & cooling_schedule )

Set cooling schedule.

void julian::SimulatedAnnealing::setExponentialCooling	(	double	Tstart,
		double	Tend,
		double	param
	)

Calculates exponential cooling schedule.

Cooling schedule is calculating basing on Tstart, Tend and step provided by an user. The Schedule is $[T_{start}, \frac{T_{start}}{\text{step}}, \frac{T_{start}}{\text{step}^2}, \frac{T_{start}}{\text{step}^3},..., T_{end} ]$

Examples:: simulatedAnnealingExample.cpp.

void julian::SimulatedAnnealing::setLinearCooling	(	double	Tstart,
		double	Tend,
		double	step
	)

Calculates linear cooling schedule.

Cooling schedule is calculating basing on Tstart, Tend and step provided by an user. The Schedule is $[T_{start}, T_{start} - \text{step}, T_{start} - 2\text{step}, T_{start}-3\text{step},..., T_{end} ]$

double julian::SimulatedAnnealing::takeStep ( double x )

Calculate the new state.

std::vector< double > julian::SimulatedAnnealing::takeStep ( std::vector< double > x )

Calculate the new state.

Member Data Documentation

std::vector<double> julian::SimulatedAnnealing::cooling_schedule_

private

Cooling schedule.

SmartPointer<UniformRNG> julian::SimulatedAnnealing::rng_

private

Random number generator used in acceptance of new state.

SmartPointer<RandomVariable> julian::SimulatedAnnealing::step_

private

Distribution used in picking of neighbour state.

The documentation for this class was generated from the following files:

C:/Unix/home/OEM/jULIAN/src/mathematics/numericalAlgorithms/simulatedAnnealing.hpp
C:/Unix/home/OEM/jULIAN/src/mathematics/numericalAlgorithms/simulatedAnnealing.cpp

Public Member Functions

Private Attributes

Detailed Description

Constructor & Destructor Documentation

Member Function Documentation

Member Data Documentation