Routines for finding minima of arbitrary one- or multi- dimensional functions. More...
Classes | |
| class | julian::SimulatedAnnealing |
| Class implements Simulated Annealing minimizer. More... | |
Enumerations | |
| enum | julian::DerivativeMinimizer { julian::DerivativeMinimizer::FLETCHER_REEVES, julian::DerivativeMinimizer::POLAK_RIBIERE, julian::DerivativeMinimizer::BROYDEN_FLETCHER, julian::DerivativeMinimizer::STEEPEST_DESCENT } |
| Types of multi-dimension minimizer that requires gradient of function. More... | |
| enum | julian::Minimizer1d { julian::Minimizer1d::GOLDEN_SECTION_MINIMIZER, julian::Minimizer1d::BRENT_MINIMIZER, julian::Minimizer1d::QUAD_GOLDEN } |
| Types of 1d minimizers algorithms. More... | |
| enum | julian::NonDerivativeMinimizer { julian::NonDerivativeMinimizer::NELDER_MEAD_SIMPLEX, julian::NonDerivativeMinimizer::RANDOM_NELDER_MEAD_SIMPLEX } |
| Types of multi-dimension minimizer that does not require derivative of function. More... | |
Functions | |
| template<typename F , typename dF , typename FdF > | |
| std::vector< double > | julian::derivativeMinimizer (F f, dF df, FdF fdf, std::vector< double > x_init, DerivativeMinimizer type, double step_size=0.1, double tol=1e-4, double abs=1e-6, unsigned int max_iter=200) |
| Multidimension minimizer that requires derivative of function. More... | |
| template<typename F > | |
| std::vector< double > | julian::derivativeMinimizer (F f, std::vector< double > x_init, DerivativeMinimizer type, double step_size=0.1, double tol=1e-4, double increment=1e-5, double abs=1e-6, unsigned int max_iter=200) |
| Multidimension minimizer that requires derivative of function. More... | |
| template<typename F > | |
| double | julian::minimizer1d (F f, double x_lo, double x_hi, double guess, double precision, int number_of_iterations, Minimizer1d t) |
| Function finds minimum of provided one-argument function. More... | |
| template<typename F > | |
| std::vector< double > | julian::nonDerivativeMinimizer (F f, std::vector< double > x_init, NonDerivativeMinimizer t, double abs=1e-3, int number_of_iterations=100) |
| Multi-dimension minimizer that does not require derivative of function. More... | |
Detailed Description
Routines for finding minima of arbitrary one- or multi- dimensional functions.
The minimum finding routines can be divided into two groups:
- derivative-free optimization: Algorithms that that does not use derivative information in the classical sense to find optimal solutions (see julian::NonDerivativeMinimizer)
derivative-based optimization: Algorithms basing on the calculation of gradient of cost function (see DerivativeMinimizer)
Good introduction to minimization techniques see Chapter 10 of [4] and Chapter 6 of [33].
Enumeration Type Documentation
|
strong |
Types of multi-dimension minimizer that requires gradient of function.
The function may use one of algorithms defined below:
Fletcher-Reeves conjugate gradient
An initial search direction p is chosen using the gradient, and line minimization is carried out in that direction. The accuracy of the line minimization is specified by the parameter tol. The minimum along this line occurs when the function gradient g and the search direction p are orthogonal. The line minimization terminates when
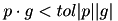 . The search direction is updated using the Fletcher-Reeves formula
. The search direction is updated using the Fletcher-Reeves formula 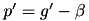 g where
g where 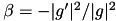 ,
,Polak Ribiere conjugate gradient
Method similar ot Fletcher-Reeves, differing only in the choice of the coefficient
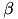 .
. ![\[\beta = \frac{g'(g-g')}{g^2} \]](form_152.png)
Broyden-Fletcher-Goldfarb-Shanno
BFGS method belongs to quasi-Newton methods. In quasi-Newton methods, the Hessian matrix of second derivatives doesn't need to be evaluated directly. Instead, the Hessian matrix is approximated using updates specified by gradient evaluations (or approximate gradient evaluations).
This version of this minimizer is the most efficient version available, and is a faithful implementation of the line minimization scheme described in Fletcher’s Practical Methods of Optimization ([34])
Steepest Descent
Algorithm follows the downhill gradient of the function. After the step was made the algorithm calculates function value for new position. If new value of cost function is smaller step-size is doubled. If the downhill step leads to a higher function value then the algorithm backtracks and the step size is decreased using the parameter tol.
For more information see [34] , 10.6-10.7 chapter of [4] and GSL Docs ( link).
| Enumerator | |
|---|---|
| FLETCHER_REEVES |
Fletcher-Reeves conjugate gradient. |
| POLAK_RIBIERE |
Polak-Ribiere conjugate gradient. |
| BROYDEN_FLETCHER |
Broyden-Fletcher-Goldfarb-Shanno. |
| STEEPEST_DESCENT |
Steepest Descent. |
|
strong |
Types of 1d minimizers algorithms.
The function may use one of three algorithms defined below:
Golden Section minimizer
The golden section algorithm is the simplest method of bracketing the minimum of a function. It is the slowest algorithm provided by the library, with linear convergence.
On each iteration, the algorithm first compares the subintervals from the endpoints to the current minimum. The larger subinterval is divided in a golden section (using the famous ratio
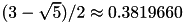 and the value of the function at this new point is calculated. The new value is used with the constraint
and the value of the function at this new point is calculated. The new value is used with the constraint 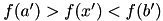 to a select new interval containing the minimum, by discarding the least useful point. This procedure can be continued indefinitely until the interval is sufficiently small. Choosing the golden section as the bisection ratio can be shown to provide the fastest convergence for this type of algorithm.
to a select new interval containing the minimum, by discarding the least useful point. This procedure can be continued indefinitely until the interval is sufficiently small. Choosing the golden section as the bisection ratio can be shown to provide the fastest convergence for this type of algorithm.Brent's minimizer
The Brent minimization algorithm combines a parabolic interpolation with the golden section algorithm. This produces a fast algorithm which is still robust.
Brent-Gill-Murray algorithm
This is a variant of Brent’s algorithm which uses the safeguarded step-length algorithm of Gill and Murray.
For more information see Chapter 10 of Numerical Recipes [4] and GSL Docs ( link).
| Enumerator | |
|---|---|
| GOLDEN_SECTION_MINIMIZER |
Golden Section minimizer. |
| BRENT_MINIMIZER |
Brent's minimizer. |
| QUAD_GOLDEN |
Brent-Gill-Murray algorithm. |
|
strong |
Types of multi-dimension minimizer that does not require derivative of function.
The function may use one of two algorithm defined below:
Nelder-Mead Simplex
The Nelder–Mead method or downhill simplex method or amoeba method is a commonly applied numerical method used to find the minimum or maximum of an objective function in a multidimensional space. It is applied to non-linear optimization problems for which derivatives may not be known.
Random Nelder-Mead Simplex
This method is a variant of Nelder-Mead Simplex which initialises the simplex around the starting point x using a randomly-oriented set of basis vectors instead of the fixed coordinate axes
For more information see Chapter 10 of Numerical Recipes [4], original paper [19] and GSL Docs ( link).
| Enumerator | |
|---|---|
| NELDER_MEAD_SIMPLEX |
Nelder-Mead Simplex. |
| RANDOM_NELDER_MEAD_SIMPLEX |
Random Nelder-Mead Simplex. |
Function Documentation
| std::vector<double> julian::derivativeMinimizer | ( | F | f, |
| dF | df, | ||
| FdF | fdf, | ||
| std::vector< double > | x_init, | ||
| DerivativeMinimizer | type, | ||
| double | step_size = 0.1, |
||
| double | tol = 1e-4, |
||
| double | abs = 1e-6, |
||
| unsigned int | max_iter = 200 |
||
| ) |
Multidimension minimizer that requires derivative of function.
- Parameters
-
f Functor with overloaded: double operator(vector<dobule>), that calculates the value of the optimized function. df Functor with overloaded: vector<dobule> operator(vector<dobule>), that calculates the gradient of the optimized function. fdf Functor with overloaded: pair<double,vector> operator(vector<dobule>), that calculates the value and the gradient of the optimized function. x_init initial point type Type of algorithm (see DerivativeMinimizer) step_size The size of the first trial step tol line minimization parameter; interpretation of tol parameter depends on the algorithm used abs The function tests the norm of the gradient against the absolute tolerance abs. max_iter Maximal number of iterations
- Returns
- minimum of the function
- Remarks
- Class uses algorithms implemented in GSL
| std::vector<double> julian::derivativeMinimizer | ( | F | f, |
| std::vector< double > | x_init, | ||
| DerivativeMinimizer | type, | ||
| double | step_size = 0.1, |
||
| double | tol = 1e-4, |
||
| double | increment = 1e-5, |
||
| double | abs = 1e-6, |
||
| unsigned int | max_iter = 200 |
||
| ) |
Multidimension minimizer that requires derivative of function.
Function calculates the gradient numerically using forward differentiation scheme with increment of argument provided.
- Parameters
-
f Functor with overloaded: double operator(vector<dobule>), that calculates the value of the optimized function. x_init initial point type Type of algorithm (see DerivativeMinimizer) step_size The size of the first trial step tol line minimization parameter; interpretation of tol parameter depends on the algorithm used increment increment of argument used in numerical differentiating abs The function tests the norm of the gradient against the absolute tolerance abs. max_iter Maximal number of iterations
- Returns
- minimum of the function
- Remarks
- Class uses algorithms implemented in GSL
| double julian::minimizer1d | ( | F | f, |
| double | x_lo, | ||
| double | x_hi, | ||
| double | guess, | ||
| double | precision, | ||
| int | number_of_iterations, | ||
| Minimizer1d | t | ||
| ) |
Function finds minimum of provided one-argument function.
Function finds minimum of provided one-argument function. The minimum is found in interval (x_lo, x_hi)
- Parameters
-
f Functor for which root is searched. x_lo Lower bound of interval x_hi Upper bound of interval guess initial guess for the minimum. precision Algorithm finds minimum satisfying condition 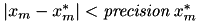
number_of_iterations A user-specified maximum number of iterations t type of minimizer see julian::Minimizer1d
- Returns
- Abscissa of minimum of function f.
- Remarks
- Function uses algorithms implemented in GSL
| std::vector<double> julian::nonDerivativeMinimizer | ( | F | f, |
| std::vector< double > | x_init, | ||
| NonDerivativeMinimizer | t, | ||
| double | abs = 1e-3, |
||
| int | number_of_iterations = 100 |
||
| ) |
Multi-dimension minimizer that does not require derivative of function.
- Parameters
-
f Functor being minimized taking std::vector<double> as argument x_init initial guess t minimizer type, see julian::NonDerivativeMinimizer abs Optimizer test the value of the function against the absolute tolerance (abs) to determine if algorithm should stop number_of_iterations A user-specified maximum number of iterations
- Returns
- std::vector representing point where f has minimum value
- Remarks
- Function uses algorithms implemented in GSL


 1.8.11
1.8.11