Numerical Algorithms

Numerical algorithms: root-finders, minimizers, integral calculators etc. More...

Modules
	Optimization algorithms
	Routines for finding minima of arbitrary one- or multi- dimensional functions.
	Root-Finding algorithms
	Routines used to find the argumen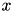t that .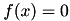
	GSL function adapters
	Wrappers for GSL functions.

Classes
class	julian::QuadraticProgrammingSolver
	Quadratic Programming Solver. More...

Enumerations
enum	julian::Integration {   julian::Integration::NON_ADAPTIVE_GAUSS_KRONROD, julian::Integration::ADAPTIVE_GAUSS_KRONROD, julian::Integration::ADAPTIVE_GAUSS_KRONROD_WITH_SINGULARITIES, julian::Integration::ADAPTIVE_GAUSS_KRONROD_INFINITE_RANGE,   julian::Integration::ADAPTIVE_GAUSS_KRONROD_UPPER_INFINITE, julian::Integration::ADAPTIVE_GAUSS_KRONROD_LOWER_INFINITE }
	Types of integrating algorithms. More...

Functions
template<typename F >
double	julian::integrate (F f, double x_lo, double x_hi, double precision_abs, double precision_rel, int n, Integration t)
	Function calculates integral. More...

Detailed Description

Numerical algorithms: root-finders, minimizers, integral calculators etc.

Most of numerical algorithms gathered in this module comes from GNU Scientific Library (GSL Manual).

The manual of GSL contains brief introduction description of each algorithm with a rich list of references and recommendations for further reading. Still Numerical Recipes([4]) should be considered as best introductory book about numerical analysis. The book covers wide range of topics from standard problems (interpolation, integration etc) to more advanced subjects. Virtually all methods discussed in the book are implemented with code printed in the book.

Another books covering subject of numerical techniques are: Computational Physics [33] and Introductory computational physics [1].

Enumeration Type Documentation

enum julian::Integration

strong

Types of integrating algorithms.

The function uses Gauss-Kronrod algorithm in six variants:

• non adaptive Gauss-Kronrod

The QNG algorithm is a non-adaptive procedure which uses fixed Gauss-Kronrod-Patterson abscissae to sample the integrand at a maximum of 87 points.

• adaptive Gauss-Kronrod

The QAG algorithm is a simple adaptive integration procedure. The integration region is divided into subintervals, and on each iteration the subinterval with the largest estimated error is bisected. This reduces the overall error rapidly, as the subintervals become concentrated around local difficulties in the integrand.

• adaptive Gauss-Kronrod with Singularities

The QAGS algorithm combines adaptive bisection with the Wynn epsilon-algorithm to speed up the integration of many types of integrable singularities.

• adaptive Gauss-Kronrod on infinite range

Algorithm computes the integral of the function f over the infinite interval 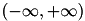. The integral is mapped onto the semi-open interval (0,1] using the transformation x = (1-t)/t. It is then integrated using the QAGS algorithm.

• adaptive Gauss-Kronrod solving improper integral with infinity as a upper limit of integration

Algorithm computes the integral of the function f over the semi-infinite interval 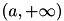. The integral is mapped onto the semi-open interval (0,1] using the transformation x = a + (1-t)/t,

• adaptive Gauss-Kronrod solving improper integral with infinity as a lower limit of integration

Algorithm computes the integral of the function f over the semi-infinite interval 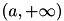. The integral is mapped onto the semi-open interval (0,1] using the transformation x = b - (1-t)/t.

For more information see Chapter 4 of Numerical Recipes [4] and manual of GNU Scientific Library (link).

Enumerator
NON_ADAPTIVE_GAUSS_KRONROD	non adaptive Gauss-Kronrod
ADAPTIVE_GAUSS_KRONROD	adaptive Gauss-Kronrod
ADAPTIVE_GAUSS_KRONROD_WITH_SINGULARITIES	adaptive Gauss-Kronrod with Singularities
ADAPTIVE_GAUSS_KRONROD_INFINITE_RANGE	adaptive Gauss-Kronrod on infinite range
ADAPTIVE_GAUSS_KRONROD_UPPER_INFINITE	adaptive Gauss-Kronrod solving improper integral with infinity as a upper limit of integration
ADAPTIVE_GAUSS_KRONROD_LOWER_INFINITE	adaptive Gauss-Kronrod solving improper integral with infinity as a lower limit of integration

Function Documentation

template<typename F >

double julian::integrate	(	F	f,
		double	x_lo,
		double	x_hi,
		double	precision_abs,
		double	precision_rel,
		int	n,
		Integration	t
	)

Function calculates integral.

Function calculates the integral of provided function for a given interval.

Parameters

f	Functor representing integrated function.
x_lo	Lower bound of interval. Not needed for Integration::ADAPTIVE_GAUSS_KRONROD_INFINITE_RANGE and Integration::ADAPTIVE_GAUSS_KRONROD_LOWER_INFINITE
x_hi	Upper bound of interval. Not needed for Integration::ADAPTIVE_GAUSS_KRONROD_INFINITE_RANGE and Integration::ADAPTIVE_GAUSS_KRONROD_UPPER_INFINITE
precision_abs	absolute error limits
precision_rel	relative error limits.
n	order of Gaussian Quadrature
t	Type of algorithm. See julian::Integration

Returns

Integrates f function on given interval

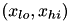
Remarks

Class uses algorithms implemented in GSL