simulatedAnnealingExample.cpp
This example show how to use simulated annealing algorithm to find minimum. We used Rosenbrock function as test function.Rosenbrock function is a non-convex function, introduced by Howard H. Rosenbrock in 1960, which is used as a performance test problem for optimization algorithms.[1] It is also known as Rosenbrock's valley or Rosenbrock's banana function. See below.
![\[f(x,y)=(a-x)^{2}+b(y-x^{2})^{2}\]](form_6.png)
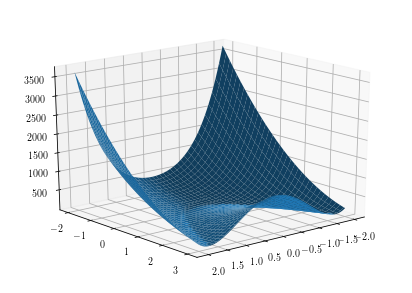
It has a global minimum at 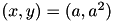 .
.
Below we see output of programme
a = 1.00000 Simulation annealing solution 0.98294 0.96559 Analytic solution 1.00000 1.00000 a = 1.50000 Simulation annealing solution 1.50252 2.25793 Analytic solution 1.50000 2.25000 a = 2.00000 Simulation annealing solution 1.99728 3.98907 Analytic solution 2.00000 4.00000 a = 2.50000 Simulation annealing solution 2.50729 6.28663 Analytic solution 2.50000 6.25000 a = 3.00000 Simulation annealing solution 3.00278 9.01678 Analytic solution 3.00000 9.00000 a = 3.50000 Simulation annealing solution 3.49863 12.24010 Analytic solution 3.50000 12.25000 a = 4.00000 Simulation annealing solution 4.00127 16.00967 Analytic solution 4.00000 16.00000 a = 4.50000 Simulation annealing solution 4.50142 20.26290 Analytic solution 4.50000 20.25000 a = 5.00000 Simulation annealing solution 4.99228 24.92404 Analytic solution 5.00000 25.00000 a = 5.50000 Simulation annealing solution 5.49660 30.21293 Analytic solution 5.50000 30.25000 a = 6.00000 Simulation annealing solution 6.01119 36.13496 Analytic solution 6.00000 36.00000 a = 6.50000 Simulation annealing solution 6.50430 42.30595 Analytic solution 6.50000 42.25000 a = 7.00000 Simulation annealing solution 6.99176 48.88552 Analytic solution 7.00000 49.00000 a = 7.50000 Simulation annealing solution 7.50189 56.27824 Analytic solution 7.50000 56.25000 a = 8.00000 Simulation annealing solution 7.99463 63.91385 Analytic solution 8.00000 64.00000 a = 8.50000 Simulation annealing solution 8.50629 72.35679 Analytic solution 8.50000 72.25000 a = 9.00000 Simulation annealing solution 9.00486 81.08827 Analytic solution 9.00000 81.00000 a = 9.50000 Simulation annealing solution 9.51114 90.46345 Analytic solution 9.50000 90.25000
#include <juliant.hpp>
using namespace julian;
int main() {
//
// Setting random number generator
//
Tausworthe rng;
UniformDistribution u(-1.0, 1.0);
CustomRandomVariable r(u, rng);
//
// Setting simulated annealing
//
SimulatedAnnealing sim(rng, r);
sim.setExponentialCooling(100.0, 0.05, 0.02);
for (double a = 1.0; a < 10.0; a += 0.5) {
auto rosenbrock = [a](std::vector<double> x)->double {
return std::pow(a-x.at(0), 2) + 100.0*std::pow(x.at(1)-std::pow(x.at(0), 2), 2);
};
//
// Defining distribution for probability accept. We choose Boltzmann distribution
//
auto boltzmann = [](double E, double E_new, double T)->double {
return -(E_new-E) / T;
};
//
// Setting initial guess and solving optimization problem
//
std::vector<double> x_init {10.0, 10.0};
std::cout << std::fixed << std::setprecision(5);
std::cout << "a = " << a << std::endl;
std::cout << "Simulation annealing solution " << res[0] << " " << res[1] << std::endl;
std::cout << "Analytic solution " << a << " " << a*a << std::endl << std::endl;
}
}


 1.8.11
1.8.11