Routines used to find the argument 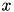 that
that 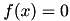 .
More...
.
More...
Enumerations | |
| enum | julian::BracketingRootFinder { julian::BracketingRootFinder::BISECTION, julian::BracketingRootFinder::FALSEPOS, julian::BracketingRootFinder::BRENT_DEKKER } |
| Types of bracketing algorithms. More... | |
| enum | julian::DerivativeRootFinder { julian::DerivativeRootFinder::NEWTON_RAPHSON, julian::DerivativeRootFinder::SECANT, julian::DerivativeRootFinder::STEFFENSEN } |
| Types of root finding algorithms using derivatives. More... | |
Functions | |
| template<typename T > | |
| double | julian::bracketingRootFinder (T f, double x_lo, double x_hi, BracketingRootFinder type, double precision=1e-12, int max_iter=100) |
| Function finds roots using bracketing algorithms. More... | |
| template<typename T , typename U > | |
| double | julian::derivativeRootFinder (T f, U df, double x_0, DerivativeRootFinder type, double precision=1e-12, int max_iter=100) |
| Function finds roots basing on derivative. More... | |
| template<typename T > | |
| double | julian::derivativeRootFinder (T f, double x_0, DerivativeRootFinder type, double precision=1e-12, int max_iter=100, double h=1e-6) |
| Function finds roots basing on derivative. More... | |
Detailed Description
Routines used to find the argument 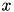 that
that 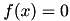 .
.
The root-finding routines can be divided into two groups:
- derivative-free: Algorithms that that does not use derivative information in the classical sense to find solutions. Usually those are bracketing algorithms
- derivative-based: Algorithms basing on the calculation of gradient.
Enumeration Type Documentation
|
strong |
Types of bracketing algorithms.
The function may use one of three algorithm defined below:
The bisection method
The bisection method in mathematics is a root-finding method that repeatedly bisects an interval and then selects a subinterval in which a root must lie for further processing.
Method of False Position An algorithm for finding roots which retains that prior estimate for which the function value has opposite sign from the function value at the current best estimate of the root. Using the two-point form of the line
![\[ y-y_1=(f(x_{n-1})-f(x_1))/(x_{n-1}-x_1)(x_n-x_1) \]](form_142.png)
with
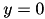 , using
, using 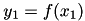 , and solving for
, and solving for 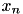 therefore gives the iteration
therefore gives the iteration ![\[x_n=x_1-(x_{n-1}-x_1)/(f(x_{n-1})-f(x_1))f(x_1)\]](form_146.png)
. For more information Wikipedia article.
- Brent-Dekker Method Brent's method is a root-finding algorithm which combines root bracketing, bisection, and inverse quadratic interpolation. For more information Wikipedia article.
For more information see Chapter 9 of Numerical Recipes [4].
| Enumerator | |
|---|---|
| BISECTION |
The bisection method. |
| FALSEPOS |
Method of False Position. |
| BRENT_DEKKER |
Brent-Dekker Method. |
|
strong |
Types of root finding algorithms using derivatives.
The function may use one of three algorithm defined below:
- Newton Raphson method
The algorithm begins with an initial guess for the location of the root. On each iteration, a line tangent to the function f is drawn at that position. The point where this line crosses the x-axis becomes the new guess. The iteration is defined by the following sequence,
![\[x_{i+1} = x_i - \frac{f(x_i)}{f'(x_i)}\]](form_153.png)
- Secant method
The secant method is a simplified version of Newton’s method which does not require the computation of the derivative on every step. On its first iteration the algorithm begins with Newton’s method, using the derivative to compute a first step,
![\[x_1 = x_0 - \frac{f(x_0)}{f'(x_0)}\]](form_154.png)
Subsequent iterations avoid the evaluation of the derivative by replacing it with a numerical estimate, the slope of the line through the previous two points,
![\[x_{i+1} = x_i - {f(x_i) \over f'_{est}} \mbox{where} f'_{est} = \frac{f(x_{i}) - f(x_{i-1})}{x_i - x_{i-1}} \]](form_155.png)
- Steffensen method
The Steffensen Method provides the fastest convergence of all the routines. It combines the basic Newton algorithm with an Aitken “delta-squared” acceleration. If the Newton iterates are 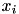 then the acceleration procedure generates a new sequence
then the acceleration procedure generates a new sequence 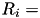 ,
,
![\[R_i = x_i - {(x_{i+1} - x_i)^2 \over (x_{i+2} - 2 x_{i+1} + x_i)}\]](form_158.png)
which converges faster than the original sequence under reasonable conditions.
Description of methods taken from GSL documentation. For more information see Chepter 9 of Numerical Recipes [4] and GSL Docs ( link).
| Enumerator | |
|---|---|
| NEWTON_RAPHSON |
Newton Raphson method. |
| SECANT |
Secant method. |
| STEFFENSEN |
Steffensen method. |
Function Documentation
| double julian::bracketingRootFinder | ( | T | f, |
| double | x_lo, | ||
| double | x_hi, | ||
| BracketingRootFinder | type, | ||
| double | precision = 1e-12, |
||
| int | max_iter = 100 |
||
| ) |
Function finds roots using bracketing algorithms.
We will say that a root is bracketed in the interval (a, b) if f(a) and f(b) have opposite signs. If the function is continuous, then at least one root must lie in that interval (the intermediate value theorem). Algorithms which proceed by bracketing a root are guaranteed to converge, but usually are slow. For more information see Chapter 9 of Numerical Recipes [4].
- Parameters
-
f Functor for which root is searched. x_lo Lower bound of interval x_hi Upper bound of interval type Type of algorithm. See julian::BracketingRootFinder precision User-specified precision (relative). When this number is reached, algorithm is stopped. Default value 1e-12. max_iter A user-specified maximum number of iterations. When this number is reached, algorithm is stopped. Default value 100.
- Returns
- Root of f function found in interval
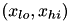
- Remarks
- Function uses algorithms implemented in GSL
| double julian::derivativeRootFinder | ( | T | f, |
| U | df, | ||
| double | x_0, | ||
| DerivativeRootFinder | type, | ||
| double | precision = 1e-12, |
||
| int | max_iter = 100 |
||
| ) |
Function finds roots basing on derivative.
The derivative root algorithms require an initial guess for the location of the root. There is no absolute guarantee of convergence—the function must be suitable for this technique and the initial guess must be sufficiently close to the root for it to work. When these conditions are satisfied then convergence is quadratic.
- Parameters
-
f Functor for which root is searched. df Functor calculating derivative of f. x_0 Initial guess type Type of algorithm. See julian::DerivativeRootFinder precision User-specified precision (relative). When this number is reached, algorithm is stopped. Default value 1e-12. max_iter A user-specified maximum number of iterations. When this number is reached, algorithm is stopped. Default value 100.
- Returns
- Root of f function
- Remarks
- Function uses algorithms implemented in GSL
| double julian::derivativeRootFinder | ( | T | f, |
| double | x_0, | ||
| DerivativeRootFinder | type, | ||
| double | precision = 1e-12, |
||
| int | max_iter = 100, |
||
| double | h = 1e-6 |
||
| ) |
Function finds roots basing on derivative.
The derivative root algorithms require an initial guess for the location of the root. There is no absolute guarantee of convergence—the function must be suitable for this technique and the initial guess must be sufficiently close to the root for it to work. When these conditions are satisfied then convergence is quadratic.
The function does not need derivative of f function. It approximates derivative using finite difference:
![\[f'(x) \approx \frac{f(x+h) - f(x)}{h}\]](form_159.png)
- Parameters
-
f Functor for which root is searched. x_0 Initial guess type Type of algorithm. See julian::DerivativeRootFinder precision User-specified precision (relative). When this number is reached, algorithm is stopped. Default value 1e-12. max_iter A user-specified maximum number of iterations. When this number is reached, algorithm is stopped. Default value 100. h increment used in numerical differentiation
- Returns
- Root of f function
- Remarks
- Function uses algorithms implemented in GSL


 1.8.11
1.8.11