Pricing engines for options. Pricing engines are classes that are used to generate the PV and Greeks for a given product using provided market model.. More...
Modules | |
| Analytical Engines | |
| Analytical pricing engines. | |
| PV and Greeks | |
| Definition of classes that are used to construct risk reports about options PV and Greeks. | |
Classes | |
| class | julian::PricingEngine |
| Interface for all pricing engines. More... | |
| class | julian::DeeplyCopyablePricingEngine< T > |
| Class uses Curiously Recurring Template Pattern to implement polymorphic copy construction in every derived class implementing PricingEngine. More... | |
Functions | |
| double | julian::prizeBlackScholes (double S, double K, double DFr, double DFq, double vol, double t, CallPut icp) |
| Function calculates prize of European option using Black-Scholes formula. More... | |
| double | julian::calculateImpliedVolatility (double S, double K, double DFr, double DFq, double prize, double t, CallPut icp) |
| Function calculates implied volatility. More... | |
| double | julian::calculateBlackScholesDelta (double S, double K, double DFr, double DFq, double vol, double t, CallPut icp) |
| Function calculates delta parameter of European option. More... | |
| double | julian::calculateStrikeFromCallDelta (double spot, double DFr, double DFq, double vol, double t, double delta) |
| Function calculates delta parameter of European option. More... | |
| double | julian::calculateStrikeFromPutDelta (double spot, double DFr, double DFq, double vol, double t, double delta) |
| Function calculates delta parameter of European option. More... | |
Detailed Description
Pricing engines for options. Pricing engines are classes that are used to generate the PV and Greeks for a given product using provided market model..
Function Documentation
| double julian::calculateBlackScholesDelta | ( | double | S, |
| double | K, | ||
| double | DFr, | ||
| double | DFq, | ||
| double | vol, | ||
| double | t, | ||
| CallPut | icp | ||
| ) |
Function calculates delta parameter of European option.
Function uses BS formula:
![\[ \begin{aligned} C & = i_{cp} \times S \times DFq \times N(i_{cp} d_{1}) \\ d_{1} & = \frac{ln(\frac{S\frac{DFq}{DFr}}{K}) + \frac{var}{2} t}{\sqrt{var}} \\ var & = vol^2 t \end{aligned}\]](form_242.png)
- Parameters
-
S asset prize K strike DFr discount factor DFq capitalization of asset prize vol volatility of asset prize t time in years icp Call/Put, equals 1 for Call and -1 for Put
- Returns
- delta of European Option paying
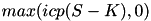at time T
| double julian::calculateImpliedVolatility | ( | double | S, |
| double | K, | ||
| double | DFr, | ||
| double | DFq, | ||
| double | prize, | ||
| double | t, | ||
| CallPut | icp | ||
| ) |
Function calculates implied volatility.
Function uses BracketingRootFinder::BRENT_DEKKER algorithm to find the value of volatility that match Black-Scholes prize with market prize. Function uses julian::prizeBlackScholes function
- Parameters
-
S asset prize K strike DFr discount factor DFq capitalization of asset prize prize option's prize t time in years icp Call/Put, equals 1 for Call and -1 for Put
- Returns
- implied volatility
| double julian::calculateStrikeFromCallDelta | ( | double | spot, |
| double | DFr, | ||
| double | DFq, | ||
| double | vol, | ||
| double | t, | ||
| double | delta | ||
| ) |
Function calculates delta parameter of European option.
Function uses BS formula:
![\[ \frac{DFq}{DFr} \times spot * exp^{ N^{-1}( delta / DFq) \times vol \times sqrt(t) - 0.5 \times vol \times vol \times t}\]](form_243.png)
where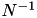 
is inverse CDF of normal distribution
- Parameters
-
spot asset prize DFr discount factor DFq capitalization of asset prize vol volatility of asset prize t time in years delta delta of call
- Returns
- strike of European option
| double julian::calculateStrikeFromPutDelta | ( | double | spot, |
| double | DFr, | ||
| double | DFq, | ||
| double | vol, | ||
| double | t, | ||
| double | delta | ||
| ) |
Function calculates delta parameter of European option.
Function uses BS formula:
![\[ \frac{DFq}{DFr} \times spot * exp^{-( N^{-1}( -delta / DFq) \times vol \times sqrt(t) - 0.5 \times vol \times vol \times t)}\]](form_245.png)
where 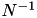is inverse CDF of normal distribution
- Parameters
-
spot asset prize DFr discount factor DFq capitalization of asset prize vol volatility of asset prize t time in years delta delta of call
- Returns
- strike of European option
| double julian::prizeBlackScholes | ( | double | S, |
| double | K, | ||
| double | DFr, | ||
| double | DFq, | ||
| double | vol, | ||
| double | t, | ||
| CallPut | icp | ||
| ) |
Function calculates prize of European option using Black-Scholes formula.
Function uses BS formula:
![\[ \begin{aligned} C & = i_{cp} (S \times DFq \times N(i_{cp} d_{1}) - K \times DFr \times N(i_{cp}d_{2})) \\ d_{1} & = \frac{ln(\frac{S\frac{DFq}{DFr}}{K}) + \frac{var}{2} t}{\sqrt{var}} \\ d_{2} & = \frac{ln(\frac{S\frac{DFq}{DFr}}{K}) - \frac{var}{2} t}{\sqrt{var}} \\ var & = vol^2 t \end{aligned}\]](form_240.png)
- Parameters
-
S asset prize K strike DFr discount factor DFq capitalization of asset prize vol volatility of asset prize t time in years icp Call/Put, equals 1 for Call and -1 for Put
- Returns
- prize of European Option paying 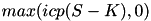at time T
