Class implements robust linear regression. More...
#include <robustRegression.hpp>

Public Types | |
| enum | type { BISQUARE, CAUCHY, FAIR, HUBER, OLS, WELSCH } |
| Robust regression types. More... | |
Public Member Functions | |
| RobustRegression () | |
| constructor More... | |
| RobustRegression (int order, RobustRegression::type t) | |
| constructor More... | |
| void | estimate (const std::vector< double > &x, const std::vector< double > &y) |
| estimates the parameters basing on provided data More... | |
| std::vector< double > | getCoefficient () const |
| return coefficients of the regression More... | |
| double | operator() (double) const |
| Operator performing calculation. More... | |
 Public Member Functions inherited from julian::DeeplyCopyableRegression< RobustRegression > Public Member Functions inherited from julian::DeeplyCopyableRegression< RobustRegression > | |
| virtual Regression * | clone () const |
| virtual copy constructor More... | |
 Public Member Functions inherited from julian::Regression Public Member Functions inherited from julian::Regression | |
| Regression () | |
| Constructor. More... | |
| virtual | ~Regression () |
| Destructor. More... | |
Private Attributes | |
| int | order_ |
| Order of polynomial. More... | |
| RobustRegression::type | type_ |
| Type of robust regression. More... | |
| std::vector< double > | coefs_ |
| Vector of coefficients. More... | |
Detailed Description
Class implements robust linear regression.
Robust regression is introduced because OLS models are often heavily influenced by the presence of outliers. Generally robust regression is estimated by minimizing the objective function
![\[\sum_i \rho(e_i) = \sum_i \rho (y_i - Y(c, x_i))\]](form_187.png)
where 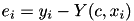 is the residual of the ith data point, and
is the residual of the ith data point, and 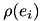 is a function that:
is a function that:
1) 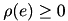
2) 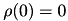
3) 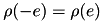
4) 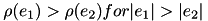
When 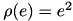 we obtain OLS estimator. To find the coefficients minimizing the objective function Iteratively Reweighed Least Squares (IRLS) algorithm is used. In this algorithm the problem of minimizing above sum is reduced to standard OLS with weighting, where weights
we obtain OLS estimator. To find the coefficients minimizing the objective function Iteratively Reweighed Least Squares (IRLS) algorithm is used. In this algorithm the problem of minimizing above sum is reduced to standard OLS with weighting, where weights 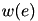 depends on error term.
depends on error term.
Apart from OLS following functions can be used:
Tukey's bi-square function
![\[ w(e) = \left\{ \begin{array}{cc} (1 - e^2)^2, & |e| \le 1 \\ 0, & |e| > 1 \end{array}\right.\]](form_196.png)
Cauchy’s function (aka Lorentzian function)
![\[ w(e) = \frac{1}{1 + e^2}\]](form_197.png)
fair regression
![\[w(e) = frac{1}{ 1 + |e|}\]](form_198.png)
OLS
![\[w(e) = 1 \]](form_199.png)
Welsch function
![\[w(e) = \exp{(-e^2)}\]](form_200.png)
- Warning
- Cauchy's function does not guarantee a unique solution.
For more information see Chapter 15.7 of [4], Robust Regression and Iteratively reweighted least squares
- Remarks
- Class uses algorithm implemented in GSL
Member Enumeration Documentation
Constructor & Destructor Documentation
|
inline |
constructor
- Note
- If no arguments are provided, order of polynomial is set to 2 and type is set to OLS.
|
inline |
constructor
Member Function Documentation
|
virtual |
estimates the parameters basing on provided data
Implements julian::Regression.
|
virtual |
return coefficients of the regression
The i-th term of vector represents coefficient of 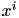
Implements julian::Regression.
|
virtual |
Operator performing calculation.
This operator returns the value for a given regressor.
Implements julian::Regression.
Member Data Documentation
|
private |
Vector of coefficients.
|
private |
Order of polynomial.
|
private |
Type of robust regression.
The documentation for this class was generated from the following files:
- C:/Unix/home/OEM/jULIAN/src/mathematics/regressions/robustRegression.hpp
- C:/Unix/home/OEM/jULIAN/src/mathematics/regressions/robustRegression.cpp


 1.8.11
1.8.11