Class implements interface for differential schemes. More...

#include <fdScheme.hpp>

Inheritance diagram for marian::FDScheme:

Public Member Functions
virtual void	setSolver (const SmartPointer< TridiagonalSolver > &solver)=0
	Provides a solver used in implicit scheme.

virtual std::vector< double >	solve (std::vector< double > f, const std::vector< SmartPointer< BoundaryCondition > > &bcs, const std::vector< double > &time_grid, const TridiagonalOperator &L)=0
	Solves PDE defined by provided linear operator L and initial and boundary conditions. More...

virtual std::vector< double >	solveAndSave (std::vector< double > f, const std::vector< SmartPointer< BoundaryCondition > > &bcs, const std::vector< double > &spatial_grid, const std::vector< double > &time_grid, const TridiagonalOperator &L, const std::string file_name)=0
	Solves PDE defined by provided linear operator L and initial and boundary conditions. Additionally saves solution to CSV file. More...

virtual std::string	info () const =0
	Returns scheme name.

virtual FDScheme *	clone () const =0
	Virtual copy constructor.

virtual	~FDScheme ()
	Deconstructor.

Detailed Description

When we solve following parabolic PDE:

$\frac{df(x,t)}{dt} = L f(x,t)$

where L is linear operator, we can use different time discretization scheme, for example in case of Forward Kolmogorov Equation:

$\begin{aligned} \text{in case of explicit scheme: }\frac{f(x_i,t_{j+1})-f(x_i,t_{j})}{t_{j+1}-t_{j}} & = \hat{L} f(x_i,t_{j}) \Rightarrow f(x_i,t_{j+1})= (I + (t_{j+1}-t_{j})\hat{L}) f(x_i,t_{j}) \\ \text{in case of explicit scheme: }\frac{f(x_i,t_{j+1})-f(x_i,t_{j})}{t_{j+1}-t_{j}} & = \hat{L} f(x_i,t_{j+1}) \Rightarrow f(x_i,t_{j})= (I - (t_{j+1}-t_{j})\hat{L}) f(x_i,t_{j+1}) \end{aligned}$

The difference between implicit scheme and explicit scheme lies in number of unknown values of on the time level. In explicit scheme we have three known values (in case of forward equation): 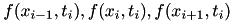$f(x_{i-1},t_{i}),f(x_{i},t_{i}),f(x_{i+1},t_{i})$ and one unknown 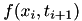$f(x_{i},t_{i+1})$ . This is why we can explicitly find the unknown values. In case of implicit we have three unknown values and one known for each time point. Solving this kind of system requires finding global solution. Because of that implicit scheme is numerically more demanding, but it is unconditionally stable in contrast to explicit scheme. For more information see [2] [5] [10] .

Member Function Documentation

virtual std::vector<double> marian::FDScheme::solve	(	std::vector< double >	f,
		const std::vector< SmartPointer< BoundaryCondition > > &	bcs,
		const std::vector< double > &	time_grid,
		const TridiagonalOperator &	L
	)

pure virtual

Parameters

f	Initial condition
bcs	Boundary conditions
time_grid	Time grid used in
L	Linear operator defining PDE

Returns: Solution in form of std::vector

Implemented in marian::ExplicitScheme, marian::ImplicitScheme, and marian::CrankNicolsonScheme.

virtual std::vector<double> marian::FDScheme::solveAndSave	(	std::vector< double >	f,
		const std::vector< SmartPointer< BoundaryCondition > > &	bcs,
		const std::vector< double > &	spatial_grid,
		const std::vector< double > &	time_grid,
		const TridiagonalOperator &	L,
		const std::string	file_name
	)

pure virtual

Parameters

f	Initial condition
bcs	Boundary conditions
spatial_grid	Spatial grid corresponding to initial conditions (used only to save the solution to CSV file)
time_grid	Time grid used for time dimension of FDM
L	Linear operator defining PDE
file_name	Name of CSV file

Returns: Solution in form of std::vector

Implemented in marian::ExplicitScheme, marian::ImplicitScheme, and marian::CrankNicolsonScheme.

The documentation for this class was generated from the following file:

C:/Unix/home/OEM/fdm/src/FDM/schemes/fdScheme.hpp

Public Member Functions

Detailed Description

Member Function Documentation