Private Attributes | Friends | List of all members
marian::TridiagonalOperator Class Reference
Finite Difference Method

TridiagonalOperator is used to define differentiating operator for PDE being solved. More...

#include <tridiagonalOperator.hpp>

Public Member Functions

Constructors
 TridiagonalOperator ()
 Default constructor.
 
 TridiagonalOperator (unsigned int size)
 Constructor defining tridiagonal operator filled with zeros. More...
 
 TridiagonalOperator (unsigned int size, double low, double mid, double upp)
 Constructor defining tridiagonal operator. More...
 
 TridiagonalOperator (const std::vector< double > &low, const std::vector< double > &mid, const std::vector< double > &upp)
 Constructor. More...
 
Getters
int size () const
 Return size of tridiagonal matrix.
 
double low (int) const
 Value of r-th row in low diagonal. More...
 
double mid (int) const
 Value of r-th row in mid diagonal. More...
 
double upp (int) const
 Value of r-th row in upp diagonal. More...
 
Setters
void setFirstRow (double, double)
 Set first row. More...
 
void setMidRow (int, double, double, double)
 Set i-th row. More...
 
void setMidRows (double, double, double)
 Set middle rows. More...
 
void setLastRow (double, double)
 Set first row. More...
 

Static Public Member Functions

Differential Operators
static TridiagonalOperator DPlus (int n, double h)
 Creates tridiagonal operator representing forward differentiating of function f. More...
 
static TridiagonalOperator DMinus (int n, double h)
 Creates tridiagonal operator representing backward differentiating of function f. More...
 
static TridiagonalOperator DZero (int n, double h)
 Creates tridiagonal operator representing central differentiating of function f. More...
 
static TridiagonalOperator DZero (const std::vector< double > &grid)
 Creates tridiagonal operator representing central differentiating of function f on non-uniform grid. More...
 
static TridiagonalOperator DPlusMinus (int n, double h)
 Creates tridiagonal operator representing central second differentiating of function f. More...
 
static TridiagonalOperator DPlusMinus (const std::vector< double > &grid)
 Creates tridiagonal operator representing central second differentiating of function f on non-uniform grid. More...
 
static TridiagonalOperator I (int n)
 Creates tridiagonal operator representing identity matrix. More...
 
static TridiagonalOperator I (const std::vector< double > &grid)
 Creates tridiagonal operator representing identity matrix. More...
 

Private Attributes

unsigned int size_
 Size of matrix.
 
std::vector< double > low_
 Lower diagonal.
 
std::vector< double > mid_
 Mid diagonal.
 
std::vector< double > upp_
 upper diagonal
 

Friends

std::ostream & operator<< (std::ostream &s, const TridiagonalOperator &A)
 Overloading of << operator. More...
 
TridiagonalOperator operator+ (const TridiagonalOperator &, const TridiagonalOperator &)
 Overloading of + operator. More...
 
TridiagonalOperator operator- (const TridiagonalOperator &, const TridiagonalOperator &)
 Overloading of - operator. More...
 
TridiagonalOperator operator* (double, const TridiagonalOperator &)
 Overloading of * operator for TridiagonalOperator and a real number. More...
 
TridiagonalOperator operator* (const TridiagonalOperator &, double)
 Overloading of * operator for TridiagonalOperator and a real number. More...
 
TridiagonalOperator operator/ (const TridiagonalOperator &, double)
 Overloading of / operator for TridiagonalOperator and a real number. More...
 
std::vector< double > operator* (const TridiagonalOperator &, std::vector< double >)
 Overloading of * operator for TridiagonalOperator and a vector of real number. More...
 

Detailed Description

TridiagonalOperator is tridiagonal matrix is a band matrix that has non-zero elements only on the main diagonal, the first diagonal below this, and the first diagonal above the main diagonal.

\[Tridiag = \begin{pmatrix}a_1 & b_1 \\c_1 & a_2 & b_2 \\& c_2 & \ddots & \ddots \\& & \ddots & \ddots & b_{n-1} \\& & & c_{n-1} & a_n\end{pmatrix}\]

As a sparse matrix having non-zero elements only on its diagonals it can be represented by three number vectors representing below lower, upper and mid diagonal.

Tridiagonal matrices are convenient way to represent finite different problem. For example, forward difference formula:

\[f''(x_i)\approx {\frac {\delta _{h}^{2}f(x_i)}{h^{2}}}={\frac {f(x_i+h)-2f(x_i)+f(x_i-h)}{h^{2}}}\]

can be represent by following matrix:

\[f''(x) \approx {\frac {f(x_i+h)-2f(x_i)+f(x_i-h)}{h^{2}}}=\frac{1}{h^2} \begin{pmatrix} -2.0 & 1.0 \\ 1.0 & -2.0 & 1.0 \\ & 1.0 & -2.0 & 1.0 \\ & & \ddots & \ddots & \ddots \\ & & 1.0 & -2.0 & 1.0 & \\ & & & 1.0 & -2.0 \end{pmatrix} \begin{pmatrix} f(x_1) \\ f(x_2) \\ f(x_3) \\ \vdots \\ f(x_{n-1}) \\ f_n\end{pmatrix} \]

where first and last row should be properly handled by boundary conditions and 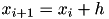$x_{i+1} = x_{i} + h$.

TridiagonalOperator class encapsulates the logic of tridiagonal matrix and provides simple methods to handle this mathematical objects. More details see [6] [13]

Constructor & Destructor Documentation

marian::TridiagonalOperator::TridiagonalOperator ( unsigned int  size = 0)
explicit
Parameters
sizeSize of tridiagonal operator
marian::TridiagonalOperator::TridiagonalOperator ( unsigned int  size,
double  low,
double  mid,
double  upp 
)
Parameters
sizeSize of tridiagonal operator
lowNumbers hold on lower diagonal
midNumbers hold on mid diagonal
uppNumbers hold on upper diagonal
marian::TridiagonalOperator::TridiagonalOperator ( const std::vector< double > &  low,
const std::vector< double > &  mid,
const std::vector< double > &  upp 
)
inline
Parameters
lowLower diagonal
midMid diagonal
uppUpper diagonal

Member Function Documentation

TridiagonalOperator marian::TridiagonalOperator::DMinus ( int  n,
double  h 
)
inlinestatic

The differential operator 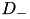$ D_{-} $ discretizes the first derivative with the backward differencing scheme

\[ \frac{\partial u}{\partial x}\Big|_{x=x_i} \approx \frac{u_{i}-u_{i-1}}{h} = D_{-} u_{i} \]

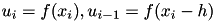
where $u_i = f(x_i), u_{i-1} = f(x_i - h)$

The matrix form is:

\[\begin{pmatrix}1 & 0 \\ -\frac{1}{h} & \frac{1}{h} & 0 \\ & -\frac{1}{h} & \frac{1}{h} & 0 \\ & & \ddots & \ddots & \ddots \\ & & & -\frac{1}{h} & \frac{1}{h} & 0 &\\ & & & & 0 & 1 \end{pmatrix}\]

Parameters
nSize of matrix
hIncrement used in differentiating scheme
TridiagonalOperator marian::TridiagonalOperator::DPlus ( int  n,
double  h 
)
inlinestatic

The differential operator 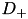$ D_{+} $ discretizes the first derivative with the forward differencing scheme

\[ \frac{\partial u}{\partial x}\Big|_{x=x_i} \approx \frac{u_{i+1}-u_{i}}{h} = D_{+} u_{i} \]

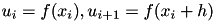
where $u_i = f(x_i), u_{i+1} = f(x_i + h)$

The matrix form is:

\[\begin{pmatrix} 1 & 0 \\ 0 & -\frac{1}{h} & \frac{1}{h} \\ & 0 & -\frac{1}{h} & \frac{1}{h} \\ & & \ddots & \ddots & \ddots \\ & & & 0 & -\frac{1}{h} & \frac{1}{h} & \\ & & & & 0 & 1 \end{pmatrix}\]

Parameters
nSize of matrix
hIncrement used in differentiating scheme
TridiagonalOperator marian::TridiagonalOperator::DPlusMinus ( int  n,
double  h 
)
inlinestatic

The differential operator 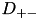$ D_{+-} $ discretizes the second derivative with the central differencing scheme

\[ \frac{\partial^2 u}{\partial x^2}\Big|_{x=x_i} \approx \frac{u_{i+1} - 2u_{i}+u_{i-1}}{h^2} = D_{+-} u_{i} \]

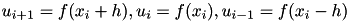
where $u_{i+1} = f(x_{i}+h), u_{i} = f(x_i), u_{i-1} = f(x_i - h)$

The matrix form is:

\[\begin{pmatrix} 1 & 0 \\ \frac{1}{h^2} & -\frac{2}{h^2} & \frac{1}{h^2} \\ & \frac{1}{h^2} & -\frac{2}{h^2} & \frac{1}{h^2} \\ & & \ddots & \ddots & \ddots \\ & & & \frac{1}{h^2} & -\frac{2}{h^2}& \frac{1}{h^2} & \\ & & & & 0 & 1 \end{pmatrix}\]

Parameters
nSize of matrix
hIncrement used in differenting scheme
TridiagonalOperator marian::TridiagonalOperator::DPlusMinus ( const std::vector< double > &  grid)
inlinestatic

The differential operator 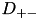$ D_{+-} $ discretizes the second derivative with the central differencing scheme

\[ \frac{\partial^2 u}{\partial x^2}\Big|_{x=x_i} \approx 2\frac{h_i u_{i+1} - (h_{i+1} + h_i) u_i + h_{i+1}u_{i-1} }{ h_i h_{i+1} (h_i+h_{i+1})} = D_{0} u_{i} \]

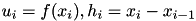
where $u_i = f(x_i), h_i = x_i - x_{i-1}$

The matrix form is:

\[\begin{pmatrix} 1& 0 \\ \frac{2h_{1}}{h_0 h_{1}(h_0+h_{1})} & -\frac{2(h_1 + h_0)}{h_0 h_{1}(h_0+h_{1})} & \frac{2h_0}{h_0 h_{1}(h_0+h_{1})} \\ & \frac{2h_{2}}{h_1 h_{2}(h_1+h_{2})} & -\frac{2(h_2 + h_1)}{h_1 h_{2}(h_1+h_{2})} & \frac{2h_1}{h_1 h_{2}(h_1+h_{2})} \\ & & \ddots & \ddots & \ddots \\ & & & \frac{2h_{n}}{h_{n-1} h_{n}(h_{n-1}+h_{n})} & -\frac{2(h_{n} + h_{n-1})}{h_{n-1} h_{n}(h_{n-1}+h_{n})} & \frac{2h_{n-1}}{h_{n-1} h_{n}(h_{n-1}+h_{n})} & \\ & & & & 0 & 1 \end{pmatrix}\]

Parameters
gridGrid used for discretization (may be non-uniform)
TridiagonalOperator marian::TridiagonalOperator::DZero ( int  n,
double  h 
)
inlinestatic

The differential operator 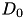$ D_{0} $ discretizes the first derivative with the central differencing scheme

\[ \frac{\partial u}{\partial x}\Big|_{x=x_i} \approx \frac{u_{i+1}-u_{i-1}}{2h} = D_{0} u_{i} \]

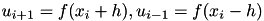
where $u_{i+1} = f(x_{i}+h), u_{i-1} = f(x_i - h)$

The matrix form is:

\[\begin{pmatrix} 1 & 0 \\ -\frac{1}{2h} &0& \frac{1}{2h} \\ & -\frac{1}{2h} &0& \frac{1}{2h} \\ & & \ddots & \ddots & \ddots \\ & & & -\frac{1}{2h} &0& \frac{1}{2h} & \\ & & & & 0 & 1 \end{pmatrix}\]

Parameters
nSize of matrix
hIncrement used in differentiating scheme
TridiagonalOperator marian::TridiagonalOperator::DZero ( const std::vector< double > &  grid)
inlinestatic

The differential operator 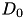$ D_{0} $ discretizes the first derivative with the central differencing scheme

\[ \frac{\partial u}{\partial x}\Big|_{x=x_i} \approx \frac{h^2_i u_{i+1} + (h^2_{i+1} - h^2_i) u_i - h^2_{i+1}u_{i-1} }{ h_i h_{i+1} (h_i+h_{i+1})} = D_{0} u_{i} \]

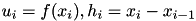
where $u_i = f(x_i), h_i = x_i - x_{i-1}$

The matrix form is:

\[\begin{pmatrix} 1& 0 \\ -\frac{h^2_{1}}{h_0 h_{1}(h_0+h_{1})} & \frac{h^2_1 - h^2_0}{h_0 h_{1}(h_0+h_{1})} & \frac{h^2_0}{h_0 h_{1}(h_0+h_{1})} \\ & -\frac{h^2_{2}}{h_1 h_{2}(h_1+h_{2})} & \frac{h^2_2 - h^2_1}{h_1 h_{2}(h_1+h_{2})} & \frac{h^2_1}{h_1 h_{2}(h_1+h_{2})} \\ & & \ddots & \ddots & \ddots \\ & & & -\frac{h^2_{n}}{h_{n-1} h_{n}(h_{n-1}+h_{n})} & \frac{h^2_{n} - h^2_{n-1}}{h_{n-1} h_{n}(h_{n-1}+h_{n})} & \frac{h^2_{n-1}}{h_{n-1} h_{n}(h_{n-1}+h_{n})} & \\ & & & & 0 & 1 \end{pmatrix}\]

Parameters
gridGrid used for discretization (may be non-uniform)
TridiagonalOperator marian::TridiagonalOperator::I ( int  n)
inlinestatic

Creates tridiagonal operator representing identity matrix. The matrix form is:

\[\begin{pmatrix} 1 & 0 \\ 0 & 1 & 0 \\ & 0 & 1 & 0 \\ & & \ddots & \ddots & \ddots \\ & & & 0 & 1 & 0 & \\ & & & & 0 & 1 \end{pmatrix}\]

Parameters
nSize of matrix
TridiagonalOperator marian::TridiagonalOperator::I ( const std::vector< double > &  grid)
inlinestatic

Creates tridiagonal operator representing identity matrix. The matrix form is:

\[\begin{pmatrix} 1 & 0 \\ 0 & 1 & 0 \\ & 0 & 1 & 0 \\ & & \ddots & \ddots & \ddots \\ & & & 0 & 1 & 0 & \\ & & & & 0 & 1 \end{pmatrix}\]

Parameters
gridGrid used for discretization (may be non-uniform)
double marian::TridiagonalOperator::low ( int  r) const
Parameters
rNumber of row
Returns
Value of r-th row in low diagonal
double marian::TridiagonalOperator::mid ( int  r) const
Parameters
rNumber of row
Returns
Value of r-th row in mid diagonal
void marian::TridiagonalOperator::setFirstRow ( double  mid,
double  upp 
)
Parameters
midValue for mid diagonal in first row
uppValue for upp diagonal in first row
void marian::TridiagonalOperator::setLastRow ( double  low,
double  mid 
)
Parameters
lowValue for lower diagonal in last row
midValue for mid diagonal in last row
void marian::TridiagonalOperator::setMidRow ( int  i,
double  low,
double  mid,
double  upp 
)
Parameters
iNumber of row
lowValue for lower diagonal in i-th row
midValue for mid diagonal in i-th row
uppValue for upper diagonal in i-th row
void marian::TridiagonalOperator::setMidRows ( double  low,
double  mid,
double  upp 
)
Parameters
lowValue for lower diagonal (except first and last row)
midValue for mid diagonal (except first and last row)
uppValue for upper diagonal (except first and last row)
double marian::TridiagonalOperator::upp ( int  r) const
Parameters
rNumber of row
Returns
Value of r-th row in upp diagonal

Friends And Related Function Documentation

TridiagonalOperator operator* ( double  x,
const TridiagonalOperator &  to 
)
friend

Operator defines left multiplication of tridiagonal operators and real number

\[ x \times \begin{pmatrix}a_1 & b_1 \\c_1 & a_2 & b_2 \\& c_2 & \ddots & \ddots \\& & \ddots & \ddots & b_{n-1} \\& & & c_{n-1} & a_n\end{pmatrix} = \begin{pmatrix}x \times a_1 & x \times b_1 \\x \times c_1 & x \times a_2 & x \times b_2 \\& x \times c_2 & \ddots & \ddots \\& & \ddots & \ddots & x \times b_{n-1} \\& & & x \times c_{n-1} & x \times a_n\end{pmatrix} \]

TridiagonalOperator operator* ( const TridiagonalOperator &  to,
double  x 
)
friend

Operator defines right multiplication of tridiagonal operators and real number

\[ \begin{pmatrix}a_1 & b_1 \\c_1 & a_2 & b_2 \\& c_2 & \ddots & \ddots \\& & \ddots & \ddots & b_{n-1} \\& & & c_{n-1} & a_n\end{pmatrix} \times x = x \times \begin{pmatrix}a_1 & b_1 \\c_1 & a_2 & b_2 \\& c_2 & \ddots & \ddots \\& & \ddots & \ddots & b_{n-1} \\& & & c_{n-1} & a_n\end{pmatrix} = \begin{pmatrix}x \times a_1 & x \times b_1 \\x \times c_1 & x \times a_2 & x \times b_2 \\& x \times c_2 & \ddots & \ddots \\& & \ddots & \ddots & x \times b_{n-1} \\& & & x \times c_{n-1} & x \times a_n\end{pmatrix} \]

std::vector<double> operator* ( const TridiagonalOperator &  A,
std::vector< double >  v 
)
friend

\[w = A \times v = \begin{pmatrix}a_1 & b_1 \\c_1 & a_2 & b_2 \\& c_2 & \ddots & \ddots \\& & \ddots & \ddots & b_{n-1} \\& & & c_{n-1} & a_n\end{pmatrix} \times \begin{pmatrix} v_1 \\ v_2 \\ v_3 \\ \vdots \\ v_{n-1} \\ v_n\end{pmatrix} = \begin{pmatrix} a_1 v_1 + v_2 b_1 \\ c_1 v_1 + a_2 v_2 + b_2 v_3 \\ \vdots \\ \vdots \\ c_{n-2} v_{n-2} + a_{n-1} v_{n-1} + b_{n-1} v_{n} \\ c_{n-1} v_{n-1} + a_n v_n \end{pmatrix} \]

Parameters
ATridiagonal matrix
vVector transformed by tridiagonal matrix A
Returns
Vector w, after transformation
TridiagonalOperator operator+ ( const TridiagonalOperator &  to1,
const TridiagonalOperator &  to2 
)
friend

Operator defines addition of tridiagonal operators

\[ \begin{pmatrix}a_1 & b_1 \\c_1 & a_2 & b_2 \\& c_2 & \ddots & \ddots \\& & \ddots & \ddots & b_{n-1} \\& & & c_{n-1} & a_n\end{pmatrix} + \begin{pmatrix}d_1 & e_1 \\f_1 & d_2 & e_2 \\& f_2 & \ddots & \ddots \\& & \ddots & \ddots & e_{n-1} \\& & & f_{n-1} & d_n\end{pmatrix} = \begin{pmatrix}a_1 + d_1 & b_1 + e_1 \\ c_1 + f_1 & a_2 + d_2 & b_2 + e_2 \\& c_2 + f_2 & \ddots & \ddots \\& & \ddots & \ddots & b_{n-1} + e_{n-1} \\& & & c_{n-1} + f_{n-1} & a_n + d_n\end{pmatrix} \]

TridiagonalOperator operator- ( const TridiagonalOperator &  to1,
const TridiagonalOperator &  to2 
)
friend

Operator defines subtraction of tridiagonal operators

\[ \begin{pmatrix}a_1 & b_1 \\c_1 & a_2 & b_2 \\& c_2 & \ddots & \ddots \\& & \ddots & \ddots & b_{n-1} \\& & & c_{n-1} & a_n\end{pmatrix} - \begin{pmatrix}d_1 & e_1 \\f_1 & d_2 & e_2 \\& f_2 & \ddots & \ddots \\& & \ddots & \ddots & e_{n-1} \\& & & f_{n-1} & d_n\end{pmatrix} = \begin{pmatrix}a_1 - d_1 & b_1 - e_1 \\ c_1 - f_1 & a_2 - d_2 & b_2 - e_2 \\& c_2 - f_2 & \ddots & \ddots \\& & \ddots & \ddots & b_{n-1} - e_{n-1} \\& & & c_{n-1} - f_{n-1} & a_n - d_n\end{pmatrix} \]

TridiagonalOperator operator/ ( const TridiagonalOperator &  to,
double  a 
)
friend

Operator defines division of tridiagonal operators by real number

\[ \begin{pmatrix}a_1 & b_1 \\c_1 & a_2 & b_2 \\& c_2 & \ddots & \ddots \\& & \ddots & \ddots & b_{n-1} \\& & & c_{n-1} & a_n\end{pmatrix} \div x = \begin{pmatrix}a_1 \div x & b_1 \div x \\ c_1 \div x & a_2 \div x & b_2 \div x \\& c_2 \div x & \ddots & \ddots \\& & \ddots & \ddots & b_{n-1} \div x \\& & & c_{n-1} \div x & a_n \div x\end{pmatrix} \]

std::ostream& operator<< ( std::ostream &  s,
const TridiagonalOperator &  A 
)
friend

Method allows to print the tridiagonal operator on console.

The documentation for this class was generated from the following files:
Generated by   doxygen 1.8.11