Set of statistical tools. More...

Functions
void	julian::stats::descriptiveStatistics (const std::vector< double > &data)
	Procedure prints the basic statistical measures. More...

double	julian::stats::mean (const std::vector< double > &data)
	Function calculates mean. More...

double	julian::stats::variance (const std::vector< double > &data)
	Function calculates variance. More...

double	julian::stats::variance (const std::vector< double > &data, const double mean)
	Function calculates variance using the provided mean. More...

double	julian::stats::stdDev (const std::vector< double > &data)
	Function calculates standard deviation. More...

double	julian::stats::stdDev (const std::vector< double > &data, const double mean)
	Function calculates standard deviation using the provided mean. More...

double	julian::stats::absDev (const std::vector< double > &data)
	Function calculates absolute deviation. More...

double	julian::stats::absDev (const std::vector< double > &data, const double mean)
	Function calculates absolute deviation using the provided mean. More...

double	julian::stats::skew (const std::vector< double > &data)
	Function calculates skew. More...

double	julian::stats::kurtosis (const std::vector< double > &data)
	Function calculates normalized kurtosis. More...

double	julian::stats::pearsonCorr (const std::vector< double > &data1, const std::vector< double > &data2)
	Function calculates Pearson correlation. More...

double	julian::stats::spearmanCorr (const std::vector< double > &data1, const std::vector< double > &data2)
	Function calculates Spearman correlation. More...

double	julian::stats::max (const std::vector< double > &data)
	Function returns the maximum value. More...

double	julian::stats::min (const std::vector< double > &data)
	Function returns the minimum value. More...

double	julian::stats::median (const std::vector< double > data)
	Function returns median. More...

double	julian::stats::percentile (const std::vector< double > data, const double &q)
	Function returns a quantile. More...

double	julian::stats::IQR (const std::vector< double > &data)
	Returns interquartile range. More...

Detailed Description

Set of statistical tools.

The basic statistical functions include routines to compute the mean, variance and standard deviation. More advanced functions allow you to calculate absolute deviations, skewness, and kurtosis as well as the median and arbitrary percentiles. The algorithms use recurrence relations to compute average quantities in a stable way, without large intermediate values that might overflow.

Function Documentation

double julian::stats::absDev ( const std::vector< double > & data )

inline

Function calculates absolute deviation.

Function calculates absolute deviation :

$absdev = {1 \over N} \sum |x_i - {\mu}|$

where

$\mu = {1 \over N} \sum x_i$

Parameters

data	Vector of doubles representing data.

Returns: Absolute deviation

double julian::stats::absDev	(	const std::vector< double > &	data,
		const double	mean
	)

inline

Function calculates absolute deviation using the provided mean.

Function calculates absolute deviation :

$absdev = {1 \over N} \sum |x_i - {mean}|$

Parameters

data	Vector of doubles representing data.
mean	Mean of the population

Returns: Absolute deviation

void julian::stats::descriptiveStatistics ( const std::vector< double > & data )

Procedure prints the basic statistical measures.

Parameters

data	Vector of doubles representing data.

double julian::stats::IQR ( const std::vector< double > & data )

inline

Returns interquartile range.

Function calculates the interquartile range (IQR) which is a measure of statistical dispersion, being equal to the difference between 75th and 25th percentiles,

Parameters

data	Vector of doubles representing data.

Returns: Returns interquartile range

double julian::stats::kurtosis ( const std::vector< double > & data )

inline

Function calculates normalized kurtosis.

Function calculates normalized kurtosis (kurtosis that of normal distribution is 0):

$kurtosis = \left( {1 \over N} \sum {\left(x_i - {\mu} \over {\sigma} \right)}^4 \right) - 3$

Parameters

data	Vector of doubles representing data.

Returns: kurtosis

double julian::stats::max ( const std::vector< double > & data )

inline

Function returns the maximum value.

Parameters

data	Vector of doubles representing data.

Returns: Maximum value of numbers in data vector

double julian::stats::mean ( const std::vector< double > & data )

inline

Function calculates mean.

Function calculates mean:

$\mu = {1 \over N} \sum x_i$

Parameters

data	Vector of doubles representing data.

Returns: mean $\mu$

double julian::stats::median ( const std::vector< double > data )

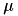
inline

Function returns median.

When the dataset has an odd number of elements the median is the value of element (n-1)/2. When the dataset has an even number of elements the median is the mean of the two nearest middle values, elements (n-1)/2 and n/2. Since the algorithm for computing the median involves interpolation this function always returns a floating-point number, even for integer data types.

Parameters

data	Vector of doubles representing data.

Returns: returns median

double julian::stats::min ( const std::vector< double > & data )

inline

Function returns the minimum value.

Parameters

data	Vector of doubles representing data.

Returns: Minimum value of numbers in data vector

double julian::stats::pearsonCorr	(	const std::vector< double > &	data1,
		const std::vector< double > &	data2
	)

inline

Function calculates Pearson correlation.

Function calculates Pearson correlation

$r = {cov(x, y) \over \sigma_x \sigma_y} = {{1 \over n-1} \sum (x_i - x) (y_i - y) \over \sqrt{{1 \over n-1} \sum (x_i - { x})^2} \sqrt{{1 \over n-1} \sum (y_i - { y})^2}}$

Parameters

data1	Vector of doubles representing first data.
data2	Vector of doubles representing second data.

Returns: Pearson correlation

double julian::stats::percentile	(	const std::vector< double >	data,
		const double &	q
	)

inline

Function returns a quantile.

The quantile is found by interpolation, using the formula

$quantile = (1 - \delta) x_i + \delta x_{i+1}$

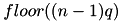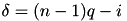where i is $floor((n - 1)q)$ and $\delta = (n-1)q - i$ .

Parameters

data	Vector of doubles representing data.
q	quantile

Returns: returns a q-th quantile

double julian::stats::skew ( const std::vector< double > & data )

inline

Function calculates skew.

Function calculates skew :

$skew = {1 \over N} \sum {\left( x_i - {\mu} \over {\sigma} \right)}^3$

Parameters

data	Vector of doubles representing data.

Returns: Skew

double julian::stats::spearmanCorr	(	const std::vector< double > &	data1,
		const std::vector< double > &	data2
	)

inline

Function calculates Spearman correlation.

Function calculates Spearman correlation

$r_{s}=1-\frac{6 \sum d_i^2}{n(n^{2}-1)}$

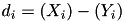where: $d_{i}= (X_{i})- (Y_{i})$ is the difference between the two ranks of each observation.

Parameters

data1	Vector of doubles representing first data.
data2	Vector of doubles representing second data.

Returns: Spearman correlation

double julian::stats::stdDev ( const std::vector< double > & data )

inline

Function calculates standard deviation.

Function calculates standard deviation :

${\sigma} = \sqrt{{1 \over (N-1)} \sum (x_i - {\mu})^2}$

where

$\mu = {1 \over N} \sum x_i$

Parameters

data	Vector of doubles representing data.

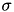
Returns: Standard deviation ${\sigma}$

double julian::stats::stdDev	(	const std::vector< double > &	data,
		const double	mean
	)

inline

Function calculates standard deviation using the provided mean.

Function calculates standard deviation using the provided mean:

${\sigma} = \sqrt{{1 \over (N)} \sum (x_i - {\mu})^2}$

Parameters

data	Vector of doubles representing data.
mean	Mean of the population

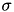
Returns: Standard deviation ${\sigma}$

double julian::stats::variance ( const std::vector< double > & data )

inline

Function calculates variance.

Function calculates :

${\sigma}^2 = {1 \over (N-1)} \sum (x_i - {\mu})^2$

where

$\mu = {1 \over N} \sum x_i$

Parameters

data	Vector of doubles representing data.

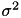
Returns: variance ${\sigma}^2$

double julian::stats::variance	(	const std::vector< double > &	data,
		const double	mean
	)

inline

Function calculates variance using the provided mean.

Function calculates variance using the provided mean:

${\sigma}^2 = {1 \over (N)} \sum (x_i - mean)^2$

Parameters

data	Vector of doubles representing data.
mean	Mean of the population

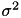
Returns: variance ${\sigma}^2$

Functions

Detailed Description

Function Documentation