Small classes and routines used in project. More...

Classes
class	marian::DataFrame
	Class used to handle data. More...

class	marian::DataEntryClerk
	Class used to provide data to julian::DataFrame. More...

class	marian::SmartPointer< T >
	Template of deep-coping smart pointer. More...

Enumerations
enum	marian::OptionType { marian::OptionType::PUT = -1, marian::OptionType::CALL = 1 }
	Types of options. More...

Functions
double	marian::normalCDF (double t)
	Normal CDF. More...

double	marian::interpolation (const std::vector< double > &x, const std::vector< double > &y, double t)
	linear local interpolation More...

std::map< std::string, EuroOpt >	marian::createEuroOpts (DataFrame df)
	Converts data stored in dataframe to European option. More...

std::map< std::string, Market >	marian::createMarkets (DataFrame df)
	Converts data stored in dataframe to market data. More...

ConvectionDiffusion	marian::mkt2process (Market mkt)
	Converts the option market data to diffusion process. More...

Detailed Description

Enumeration Type Documentation

enum marian::OptionType

strong

Enumerator
PUT	Put option.
CALL	Call option.

Function Documentation

std::map< std::string, EuroOpt > marian::createEuroOpts ( DataFrame df )

Data frame should contain following columns:

Id: String identification
Strike: double number representing strike
Tenor: double number representing tenor of option
Type: 'C' or 'P'

Parameters

df	Dataframe containing parametrization of European options

Returns: Map with options as values and ids as map's keys.

Examples:: EuroOptExample.cpp.

std::map< std::string, Market > marian::createMarkets ( DataFrame df )

Data frame should contain following columns:

Id: String identification
Spot: double number representing value of underlying
Vol: double number representing volatility
Rate: double number representing the risk free interest rate

Parameters

df	Dataframe containing parametrization of market

Returns: Map with options as values and ids as map's keys.

Examples:: EuroOptExample.cpp.

double marian::interpolation	(	const std::vector< double > &	x,
		const std::vector< double > &	y,
		double	t
	)

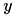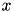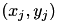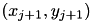The idea of linear interpolation of set of point is to approximate value $y$ at a point $x$ by a straight line passing through two data points $(x_j,y_j)$ and $(x_{j+1},y_{j+1})$ closest to 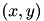$(x,y)$ . The formula for linear interpolation is:

$y = y_j + \frac{y_{j+1} - y_j}{x_{j+1} - x_j} (t-x_j)$

Parameters

x	Vector of arguments
y	Vector of values corresponding to arguments
t	Intermediate point

Returns: Value of interpolant for t

Precondition: x,y vector must be sorted.

Note: Interpolation is only defined for interval defined by the first and the last argument given. The interpolation objects do not extrapolate values outside the interval.

ConvectionDiffusion marian::mkt2process ( Market mkt )

The data defining : asset price, risk free rate and volatility of asset price. Under the assumptions of Black-Scholes model (see [4]) the price of derivative instruments satisfies the equation:

${\frac {\partial V}{\partial t}}+{\frac {1}{2}}\sigma ^{2}S^{2}{\frac {\partial ^{2}V}{\partial S^{2}}}+rS{\frac {\partial V}{\partial S}}-rV=0$

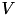where: $V$ is the price of derivative, 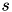$s$ asset price, 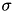$\sigma$ volatility and 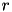$r$ is risk free rate.

After applying transformation 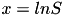$x=ln S$ the PDE will have a form:

${\frac {\partial V}{\partial t}}+{\frac {1}{2}}\sigma ^{2}{\frac {\partial ^{2}V}{\partial x^{2}}}+(r-\frac{\sigma^2}{2}){\frac {\partial V}{\partial x}}-rV=0$

Above PDE is a Backward Kolmogorov Equation associated with stochastic process: diffusion term 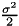$\frac{\sigma^2}{2}$ , convection term 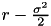$r-\frac{\sigma^2}{2}$ and decay term $r$ .

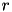double marian::normalCDF ( double t )

Function calculates Cumulative Distribution Function for standard normal distribution.

$CDF_{X}(t) = \int^{t}_{-\infty} \frac{1}{\sqrt{2\pi \sigma^{2}}}e^{-\frac{(x-\mu )^{2}}{2\sigma ^{2}}} dx$

Algorithm is basing on ERF function and its relation to Standard Normal Distribution (see formula 7.1.26 in [12])

Parameters

t argument.

Returns: Normal CDF for t

Classes

Enumerations

Functions

Detailed Description

Enumeration Type Documentation

Function Documentation