interpolationExample.cpp

Programme generates the data used to plot the examples of interpolation schemes. Programme generates the csv files containing data used to plot the examples of interpolation schemes:

• sin function
• normal distribution PDF
• function defined by formula:
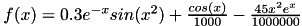
• discrete set of points (example taken from [45])

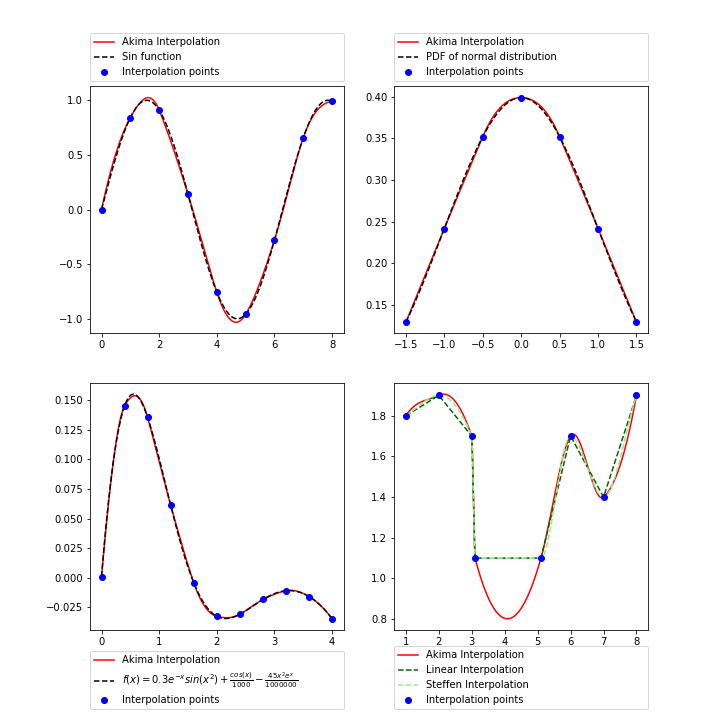
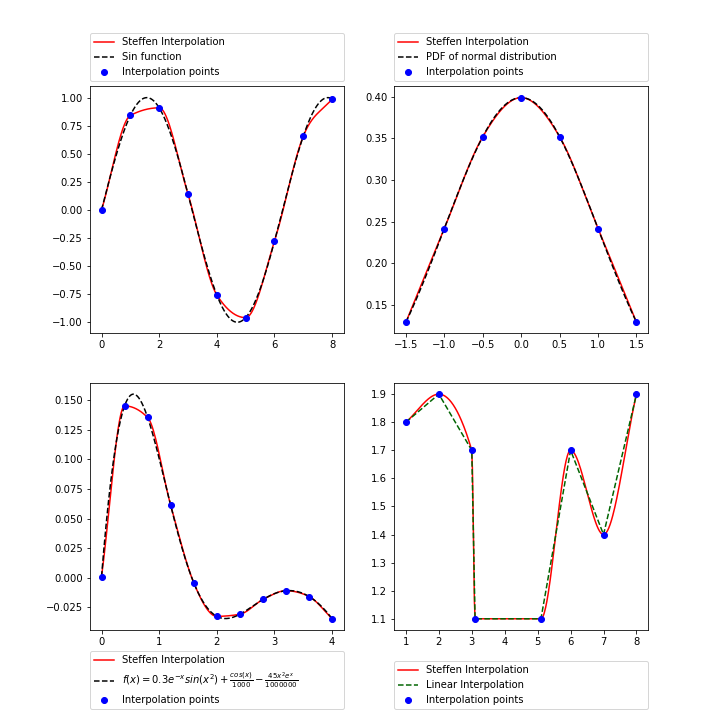
Plot aboves presents the output for AKIMA and Steffen interpolation scheme. THe plots can be generated using python script: interpolationExample.py

#include <juliant.hpp>


using namespace julian;

class InterpolationPlot {
public:
  InterpolationPlot(std::string name): name_(name) {} 

  InterpolationPlot(std::string name, std::vector<double> x, std::vector<double> y): name_(name), x_(x), y_(y) {}

  DataFrame interpolation(SmartPointer<Interpolation> inter, double step) {
    DataFrame res;
    for (double t = x_.front(); t <= x_.back(); t += step) {
       DataEntryClerk input;
       input.add("Sample", name_);
       input.add("x",  t);
       input.add("y",  inter->operator()(x_, y_, t));
       res.append(input);
    }
    return res;
  }  
  
  DataFrame interpolationPoints() {
    DataFrame res;
    for (unsigned int i = 0; i < x_.size(); i++) {
      DataEntryClerk input;
      input.add("Sample",name_);
      input.add("x",  x_[i]);
      input.add("y",  y_[i]); 
      res.append(input);
    }
    return res;
  }
  
protected:
  std::string name_;
  std::vector<double> x_;
  std::vector<double> y_;
};

template<typename F>
class InterpolationPlotWithFunc : public InterpolationPlot {
public:
  InterpolationPlotWithFunc(){};

  InterpolationPlotWithFunc(F f, std::string name, double start, double end, double step):
    InterpolationPlot::InterpolationPlot(name), f_(f) {
    for (double t = start; t<= end; t+= step) {
      x_.push_back(t);
      y_.push_back(f(t));
    }
  }

  DataFrame originalFunction(double step) {
    DataFrame df;
    for (double t = x_.front(); t<= x_.back(); t+= step) {
      DataEntryClerk input;
      input.add("Sample", name_);
      input.add("x", t);
      input.add("y", f_(t));
      df.append(input);
    }
    return df;
  }
private:
  F f_;
};



int main() {
  //
  // Creating example functions that will be used to generate interpolation points
  //
  auto func  = [](double x)->double{ return 0.3*exp(-x) * sin(x*2) + 0.001*cos(x) - 0.000045*exp(x) * x * x;};
  auto sinus = [](double x)->double{ return std::sin(x);};
  auto norm  = [](double x)->double{ NormalDistribution norm; return norm.PDF(x);};

  InterpolationPlotWithFunc<decltype(func)>  func_test(func, "custom", 0.0, 4.0, 0.4);
  InterpolationPlotWithFunc<decltype(sinus)> func_sin(sinus, "sin"   , 0.0, 8.0, 1.0);
  InterpolationPlotWithFunc<decltype(norm)>  func_norm(norm, "norm"  ,-1.5, 1.5, 0.5);

  //
  // We also define discrete set of points that will be used in interpolation 
  //
  std::vector<double> x {1.0, 2.0, 3.0, 3.1, 5.1, 6.0, 7.0, 8.0};
  std::vector<double> y {1.8, 1.9, 1.7, 1.1, 1.1, 1.7, 1.4, 1.9};
  InterpolationPlot custom_points("points", x, y);

  //
  // Saving interpolated points into csv file 
  //
  DataFrame interpolation_points;
  interpolation_points.append(func_test.interpolationPoints());
  interpolation_points.append(func_sin.interpolationPoints());
  interpolation_points.append(func_norm.interpolationPoints());
  interpolation_points.append(custom_points.interpolationPoints());
  interpolation_points.printToCsv("interpolation_points", ';');

  //
  // Saving original function (sampled with step 1e-2)  into csv file 
  //
  DataFrame original_functions;
  original_functions.append(func_test.originalFunction(0.01));
  original_functions.append(func_sin.originalFunction(0.01));
  original_functions.append(func_norm.originalFunction(0.01));
  original_functions.printToCsv("original_functions", ';');

  //
  // Defining interpolations  
  //
  std::map<std::string, SmartPointer<Interpolation> > interpolations;
  interpolations["linear"] = LinearInterpolation();
  interpolations["quadratic"] = QuadraticInterpolation();
  interpolations["cubic"] = CubicInterpolation();
  interpolations["flatbwd"] = FlatBackward();
  interpolations["flatfwd"] = FlatForward();
  interpolations["cubicSpline"] = NaturalCubicSpline();
  interpolations["akima"] = AKIMA();
  interpolations["steffen"] = SteffenInterpolation();
  interpolations["poly"] = PolynomialInterpolation();

  //
  // Gemerating interpolant for each interpolation methods and sample points
  //
  for (auto p : interpolations) {
    DataFrame results;
    results.append(func_test.interpolation(p.second, 0.02));
    results.append(func_sin.interpolation(p.second, 0.02));
    results.append(func_norm.interpolation(p.second, 0.02));
    results.append(custom_points.interpolation(p.second, 0.02));
    results.printToCsv(p.first +"_results", ';');
  }
}